數(shù)據(jù)分析中的統(tǒng)計(jì)方法各種各樣，其中回歸分析（Regression Analysis）是最經(jīng)典的方法之一。最早形式的回歸分析可以追溯到兩百多年前由德國數(shù)學(xué)家高斯提出的最小二乘法。而回歸分析也是研究時間最長和應(yīng)用最廣泛的的方法。自從產(chǎn)生以來回歸分析一直都是統(tǒng)計(jì)學(xué)家研究的一個重點(diǎn)領(lǐng)域，直到近二十多年來還有很多對回歸分析提出的各種新的改進(jìn)。
回歸分析也是機(jī)器學(xué)習(xí)（Machine Learning）中最基本的方法之一?；貧w模型一般假設(shè)響應(yīng)變量（response variable）和獨(dú)立變量（independent variables）有具體的參數(shù)化（parametric）形式的關(guān)系，而這些參數(shù)有很多成熟的方法可以去估計(jì)（比如最小二乘法），誤差分析方法也有詳細(xì)的研究。總的來說，回歸分析方法具有數(shù)據(jù)適應(yīng)性強(qiáng)，模型估計(jì)穩(wěn)定，誤差容易分析等優(yōu)良特點(diǎn)，即使在機(jī)器學(xué)習(xí)方法發(fā)展如此多種多樣的今天，依然是各個領(lǐng)域中最常用的分析方法之一。
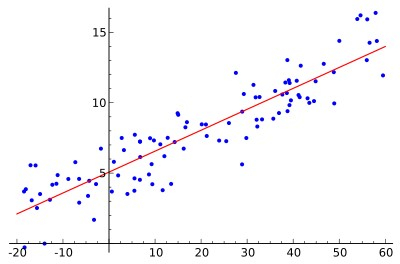
圖一：線性回歸舉例
回歸分析中最常見的線性回歸假設(shè)響應(yīng)和獨(dú)立變量間存在明顯的線性關(guān)系。如圖一所示，響應(yīng)變量（藍(lán)色點(diǎn)）的數(shù)值大致在一條（紅色）直線周圍，除了每個點(diǎn)都有的隨機(jī)誤差。線性回歸模型看似極大的簡化了響應(yīng)變量和獨(dú)立變量之間的關(guān)系，其實(shí)在實(shí)際分析中往往是最穩(wěn)定的模型。因?yàn)榫€性模型受到極端或者壞數(shù)據(jù)的影響最小。例如預(yù)測病人的住院成本，很可能出現(xiàn)其中一兩個病人會有很大的花費(fèi)，這個可能是跟病理無關(guān)的，這種病人的數(shù)據(jù)就很可能影響整個模型對于一般病人住院成本的預(yù)測。所以一個統(tǒng)計(jì)模型的穩(wěn)定性是實(shí)際應(yīng)用中的關(guān)鍵：對于相似的數(shù)據(jù)應(yīng)該得出相似的分析結(jié)果。這種穩(wěn)定性一般統(tǒng)計(jì)里用模型的方差來表示，穩(wěn)定性越好，模型的方差越小。
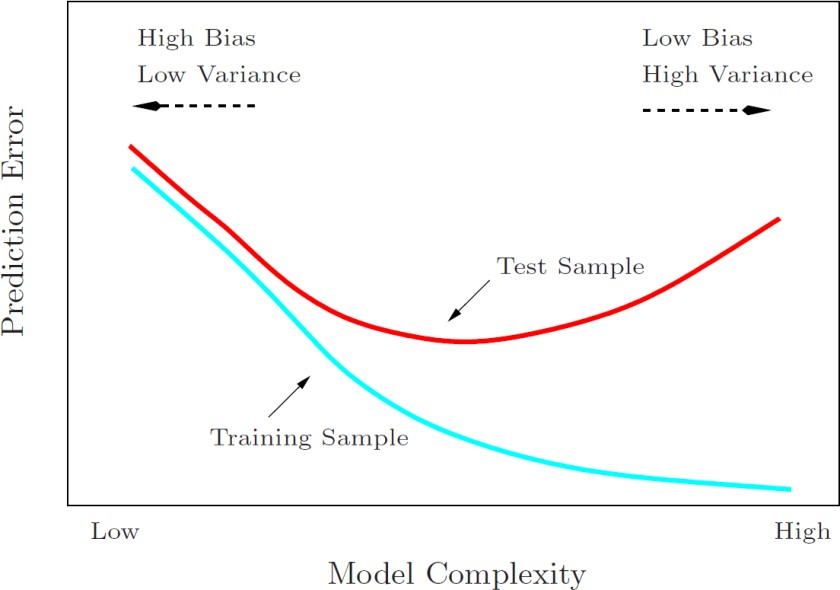
在機(jī)器學(xué)習(xí)中存在一個重要理論：方差權(quán)衡。一般常理認(rèn)為模型建立得越復(fù)雜，分析和預(yù)測效果應(yīng)該越好。而方差權(quán)衡恰恰指出了其中的弊端。復(fù)雜的模型一般對已知數(shù)據(jù)（training sample）的擬合（fitting）大過于簡單模型，但是復(fù)雜模型很容易對數(shù)據(jù)出現(xiàn)過度擬合（over-fitting）。因?yàn)樗袑?shí)際數(shù)據(jù)都會有各種形式的誤差，過度擬合相當(dāng)于把誤差也當(dāng)做有用的信息進(jìn)行學(xué)習(xí)。所以在未知數(shù)據(jù)（test sample）上的分析和預(yù)測效果會大大下降。圖二說明了方差權(quán)衡的結(jié)果。模型復(fù)雜度在最低的時候（比如線性回歸）預(yù)測的偏差比較大，但是方差很小。隨著模型復(fù)雜度的增大，對已知數(shù)據(jù)的預(yù)測誤差會一直下降（因?yàn)閿M合度增大），而對未知數(shù)據(jù)卻出現(xiàn)拐點(diǎn)，一旦過于復(fù)雜，預(yù)測方差會變大，模型變得非常不穩(wěn)定。
圖二：機(jī)器學(xué)習(xí)中的方差權(quán)衡
因此在很多實(shí)際生活應(yīng)用中，線性模型因?yàn)槠漕A(yù)測方差小，參數(shù)估計(jì)穩(wěn)定可靠，仍然起著相當(dāng)大的作用。正如上面的方差權(quán)衡所述，建立線性模型中一個重要的問題就是變量選擇（或者叫模型選擇），指的是選擇建立線性模型所用到的獨(dú)立變量的選擇。在實(shí)際問題例如疾病風(fēng)險控制中，獨(dú)立變量一般會有200 ~ 300個之多。如果使用所有的變量，很可能會出現(xiàn)模型的過度擬合。所以對變量的選擇顯得尤為重要。
傳統(tǒng)的變量選擇是采用逐步回歸法（stepwise selection），其中又分為向前（forward）和向后（backward）的逐步回歸。向前逐步是從0個變量開始逐步加入變量，而向后逐步是從所有變量的集合開始逐次去掉變量。加入或去掉變量一般按照標(biāo)準(zhǔn)的統(tǒng)計(jì)信息量來決定。這種傳統(tǒng)的變量選擇的弊端是模型的方差一般會比較高，而且靈活性較差。近年來回歸分析中的一個重大突破是引入了正則化回歸（regularized regression）的概念, 而最受關(guān)注和廣泛應(yīng)用的正則化回歸是1996年由現(xiàn)任斯坦福教授的Robert Tibshirani提出的LASSO回歸。LASSO回歸最突出的優(yōu)勢在于通過對所有變量系數(shù)進(jìn)行回歸懲罰（penalized regression）, 使得相對不重要的獨(dú)立變量系數(shù)變?yōu)?，從而排除在建模之外。
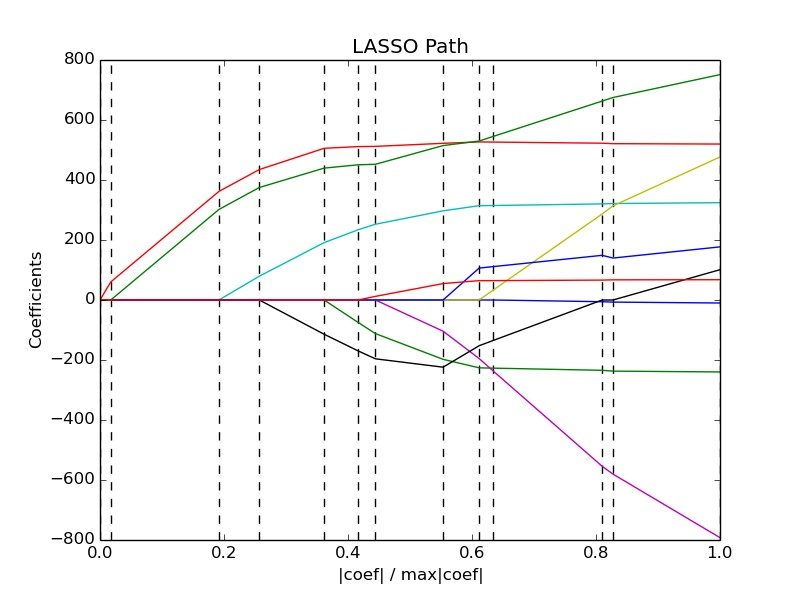
LASSO方法不同于傳統(tǒng)的逐步回歸的最大之處是它可以對所有獨(dú)立變量同時進(jìn)行處理（圖三），而不是逐步處理。這一改進(jìn)使得建模的穩(wěn)定性大大增加。除此以外，LASSO還具有計(jì)算速度快，模型容易解釋等很多優(yōu)點(diǎn)。而模型發(fā)明者Tibshirani教授也因此獲得當(dāng)年的有統(tǒng)計(jì)學(xué)諾貝爾獎之稱的考普斯總統(tǒng)獎（COPSS award）。
圖三：LASSO方法對所有變量系數(shù)的同時處理（從右向左）。利用調(diào)整（懲罰）參數(shù)的數(shù)值（從1到0），不斷有很多不重要的變量系數(shù)值變?yōu)? （即觸碰到中間的值為0的橫線）。從而達(dá)到變量選擇的目的
基于LASSO方法的線性回歸在疾病風(fēng)險控制問題上有很好的應(yīng)用。如上所述，由于疾病產(chǎn)生的獨(dú)立變量一般數(shù)量較大，且多為離散型數(shù)據(jù)，如果利用逐步回歸很可能會導(dǎo)致模型預(yù)測的方差較大。另外，LASSO方法為建立模型提供了很大的靈活性，可以很好的跟臨床診斷的一些經(jīng)驗(yàn)相結(jié)合，使得模型預(yù)測更加有的放矢。同時，模型容易解釋也使得單純的統(tǒng)計(jì)方法更能在實(shí)際醫(yī)療應(yīng)用中起到更大的作用。
